Answer:
The required result is 5 unit vertically shifted downward and
 unit horizontally shifted left.
unit horizontally shifted left.
Explanation:
Given : Graph
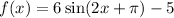
To find : In what direction and by how many units is the graph vertically and horizontally shifted?
Solution :
Vertically shift is up or down,
Vertically shifting down is shifting outside the function,
i.e, f(x)→f(x)-b
In the given graph, The graph is 5 unit vertically shifted downward as
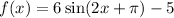 i.e, 5 unit shifted downward.
i.e, 5 unit shifted downward.
Horizontal shift is either left or right,
Horizontally shift left is shifting inside the function,
i.e, f(x)→f(x+b)
We can write the given function as
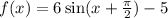
In the given graph, The graph is
 unit horizontally shifted left as
unit horizontally shifted left as
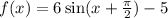 i.e,
i.e,
 unit shifted left.
unit shifted left.
Therefore, The required result is 5 unit vertically shifted downward and
 unit horizontally shifted left.
unit horizontally shifted left.