Question

A cistern can be completely drained by a pipe in 6 hours. It can be filled by two pipes in 4 hours and 5 hours, respectively. How many hours will the empty cistern take to fill if all the pipes are running? If x is the time to fill it, which of the following equations could be used to solve for t?

A. 4x + 5x - 6x = 1
B. 15x + 12x - 10x = 60
C. 4x + 5x = 20

Answer 1

let's say the pipes are "a", to drain it in 6hours, "b" to fill it up by itself in 4hours and "c" to fill it up in 5 hours.

so..."a" can drain it in 6hours, that means, in 1 hour, "a" has only done 1/6 of the job, because in 6 hours, it would have done 6/6 or 1 whole, the whole job, the cistern fully filled up, but, in 1 hour, it has only done 1/6 of that.

"b" in 1 hour, has only done 1/4 of the whole job then.
"c" in 1 hour has only done 1/5 of the whole job then.

now... let's say it took "x" hours, if we have "a", "b" and "c" running, a draining away whilst b and c filling it up.

since it takes "x" hours to fill the cistern, after 1 hour, all three have only done 1/x of the whole job.

well, let's add their rates, to see what we get then.


`\bf \begin{array}{llllllll} \cfrac{1}{4}&+&\cfrac{1}{5}&-&\cfrac{1}{6}&=&\cfrac{1}{x}\\\\ \uparrow &&\uparrow &&\uparrow &&\uparrow \\ b&&c&&a&&x \end{array}\\\\ -------------------------------\\\\ \textit{let's add the left-hand-side, using an LCD of 60} \\\\\\ \cfrac{1}{4}+\cfrac{1}{5}-\cfrac{1}{6}=\cfrac{1}{x}\implies \cfrac{15+12-10}{60}=\cfrac{1}{x}\impliedby \textit{now cross-multiplying} \\\\\\ x(15+12-10)=60(1)\implies 15x+12x-10x=60`

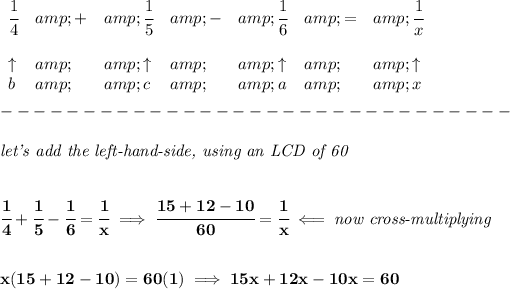
how long does it take to fill the cistern? well, just solve for "x".