What is the estimated perimeter of an ellipse if the major axis has a length of 15 ft and the minor axis has a length of 7.5 ft? Round your answer to the nearest tenth. A. 36.7 …

Question

asked Sep 11, 2018 233k views

2 Answers

Teo Choong Ping · Answer 1 · 2018-09-12T11:29:43+0000

Answer:

Option B is correct.

The estimated perimeter of an ellipse is 37.3ft

Explanation:

Given:

Length of Major-axis (2a)=15ft

Length of minor-axis (2b)=7.5ft

For an ellipse, the perimeter (P) approximately given by:

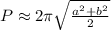$P\approx 2\pi\sqrt{(a^2+b^2)/(2)}$ , where a and b are semi major axis and semi minor axis respectively.(Use approx. value of
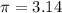$\pi =3.1 4$ )

Here, a=7.5ft and b=3.75ft, putting in above equation, we get

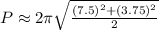
$P\approx 2\pi\sqrt{(\left (7.5\right )^2+\left (3.75\right )^2)/(2)}$

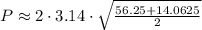
$P\approx 2\cdot 3.14\cdot \sqrt{(56.25+14.0625)/(2)}$

$P\approx\ 6.28\cdot \sqrt{(70.3125)/(2)}$

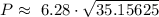
$P\approx\ 6.28\cdot √(35.15625)$

After solving the square-root we get,

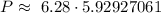
$P\approx\ 6.28\cdot5.92927061$

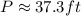$P\approx37.3ft$ .

Therefore, the estimated perimeter of an ellipse is 37.3ft.

James Iry · Answer 2 · 2018-09-16T23:31:10+0000

P = 2*pi*sqrt(a^2 +b^2/2 =

2 *3.14 * sqrt(15/2^2 +7.5/2^2/2 =

6.28 x sqrt(56.25+14.0625/2

6.28 *sqrt(35.15625)

6.28 * 5.929270613= 37.235

answer is B 37.3 feet