Question

What are the explicit equation and domain for a geometric sequence with a first term of 2 and a second term of −8?

A. an=2(-8)^n-1; all integers where n>1
B. an=2(-8)^n-1; all integers where n>0
C. an=2(-4)^n-1; all integers where n>0
D. an=2(-4)^n-1; all integers where n>1

Answer 1

The common ratio in a geometric sequence is the ratio between 2 consecutive terms:

-8/2=-4,

then the sequence is 2, -8, 32, -128, -512, 2048, ...

let
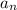
`a_n` be the nth term of the sequence, then


`a_1= 2`

`a_2=2(-4)`

`a_3=2(-4)(-4)=2(-4)^(2)`

`a_4=2(-4)(-4)(-4)=2(-4)^(3)`
.
.
.
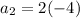
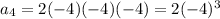
so clearly
`a_n=2(-4)^(n-1)`

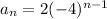
and, clearly n are integers >0, since we have a 1st term, a second term and so on... of a sequence (we do not have a "zero'th term"!

Answer:

C. an=2(-4)^n-1; all integers where n>0