Question

The 200-meter race times at a state track meet are normally distributed with a mean of 13.56 seconds and a standard deviation of 2.24 seconds. Using the Standard Normal Probabilities table, what is the approximate probability that a runner chosen at random will have a 200-meter time less than 13.5 seconds?

Answer 1

If you enter normalcdf(0, 13.5, 13.56, 2.24) in a calculator and the output result is the answer. Note that "0" is the lower limit, "13.5" is the upper limit, 13.56 is the mean, and 2.24 is the standard deviation. Less than 13.5 seconds means 0 is the lower limit and 13.56 is the upper limit.

Answer 2

P(X< 13.5) = 0.834

Explanation:

Given data:

mean of race time is
`\mu = 13.56`

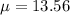
standard deviation is
`\sigma =  2.24 seconds`

we know that z is given as
`= (x-\mu)/(\sigma)`

where x is 13.5 in given problem

so probability of having runner time less than 13.5

`P(X< 13.5) = P(z< (13.5 - 13.56)/(2.24))`

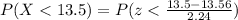
P(X< 13.5) = P(z< -0.026)

P(X< 13.5) = P(z>(1 -0.026))

P(X< 13.5) = P(z > 0.974)

from standard z table , for z = 0.974 we have 0.834

P(X< 13.5) = 0.834