Question

What are the domain and range of the logarithmic function f(x) = log7x? Use the inverse function to justify your answers.

Answer 1

I hope this helps you out

Answer 2

Answer with explanation:

The given logarithmic function whose base is, 7 is

`y=f(x)=\log_(7)x`

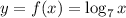
Domain of a function is defined as, set of all possible values of , x , for which ,y is defined.

`\log_(7)x=(\log x)/(\log 7)`

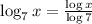
is defined for,

→ log x > 0.

⇒ x ∈ (0,∞)

And range of a function is defined as those values of y, for which x, is defined.

`y=\log_(7)x\\\\y=(\log x)/(\log 7)\\\\ \log x =y \log 7\\\\x=7^y`

So, Range = y∈ (0,∞).

The inverse of the above function can be obtained by, replacing, x by y, and y by x , in the above equation:

So, the inverse of the above function is :

`y=7^x`

Here, x ∈ (0,∞) and, y ∈ (0,∞).