Question

2 over x squared minus 9 minus 3x over x squared 5x plus 6

Answer 1

Your verbal description of the expression you're dealing with is a bit unclear, but here's what I'm assuming you're given:

`(2)/(x^2-9) - (3x)/(x^2+5x+6)`

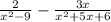
To subtract two fractions, you need a common denominator. To find out what that should be, factor the two denominators.


`(2)/((x+3)(x-3)) - (3x)/((x+2)(x+3))`

The least common denominator (LCD) must contain each distinct factor, so the LCD is
`(x+3)(x-3)(x+2)`

Now change the two fractions so they have the LCD. In this case, that means to multiply top & bottom of the first fraction by the "missing" factor (x + 2) and the second fraction's top & bottom by (x - 3).


`(2(x+3))/((x+3)(x-3)(x+2)) - (3x(x-3))/((x+3)(x-3)(x+2))`

Now, distribute the 2 in the first numerator and 3x in the second numerator (careful with that subtraction sign!) and simplify.


`(2x+4)/((x+3)(x-3)(x+2))-(3x^2-9x)/((x+3)(x-3)(x+2))`


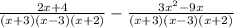
Can you finish it?