Question

Do not use your calculator for Parts 1 through 4.

Let f be the function defined as follows:

Show all your work

{ 3-x, for x < 1
f(x) = { ax^2 + bx, for 1 ≤ x < 2
{ 5x-10, for x ≥ 2

where a and b are constants

The equation in written form: f of x equals the piecewise function three minus x for x is less than one, a x squared plus b x for one is less than or equal to x is less than two, and five x minus ten for x is greater than or equal to two where a and b are constants.

1. If a = 2 and b = 3, is f continuous at x = 1? Justify your answer.

2. Find a relationship between a and b for which f is continuous at x = 1.
Hint: A relationship between a and b just means an equation in a and b.

3. Find a relationship between a and b so that f is continuous at x = 2.

4. Use your equations from parts (ii) and (iii) to find the values of a and b so that f is continuous at both x = 1 and also at x = 2?

5. Graph the piece function using the values of a and b that you have found. You may graph by hand or use your calculator to graph and copy and paste into the document.

Answer 1

You are given a piecewise function of
f(x) = 3 - x, for x < 1
= ax² + bx, for 1 ≤ x < 2
= 5x - 10, for x ≥ 2
where a and b are constants

And you are asked the following:

1. If a = 2 and b = 3, is f continuous at x = 1?
f(x) = 3 - 1 = 2 for x < 1
= (2)(1)² + (3)(1) = 5, for 1 ≤ x < 2
= 5(1) - 10 = -5 for x ≥ 2
As you can see from the answers after substituting, the following functions do not fit with the required condition. Therefore, f(1) is not continuous.

2. Find a relationship between a and b for which f is continuous at x = 1.
f(x) = 3 - 1 = 2, for x < 1
= a(1)² + b(1) = a + b, for 1 ≤ x < 2
= 5(1) - 10 = -5, for x ≥ 2
Rewriting the function with respect to a and b, we have,
f(x) = 2, for x < 1
= a + b, for 1 ≤ x < 2
= -5, for x ≥ 2

3. Find a relationship between a and b so that f is continuous at x = 2.
Same as number but instead, you are to substitute 1 with 2.
f(x) = 3 - 2 = 1, for x < 1
= a(2)² + b(2) = 4a + 2b, for 1 ≤ x < 2
= 5(2) - 10 = 0, for x ≥ 2
Rewriting it and we have
f(x) = 1, for x < 1
= 4a + 2b, for 1 ≤ x < 2
= 0, for x ≥ 2

Answer 2

The given piecewise function is
f(x) = 3 - x, x<1
= ax² + bx, 1 ≤ x < 2
= 5x - 10, x ≥ 2

Part 1:
If a = 2 and b = 3
f(1⁻) = 3 - 1 = 2⁻ (approaching 2)
f(1) = 2(1²) + (3)(1) = 5
Because
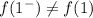
`f(1^(-)) \\e f(1)`, f(x) is not continuous at x = 1

Answer: f(x) is not continuous.

Part 2:
In order for f(x) to be continuous at x=1, we want f(1) = 2.
That is,
a + b = 2

Answer: a + b = 2

Part 3:
In order for f(x) to be continuous at x = 2,
5*2 - 10 = 0, therefore
4a + 2b = 0
2a + b = 0

Answer: 2a + b = 0

Part 4:
For f(x) to be continuous at x=1 and at x=2 requires that
a + b = 2 (1)
2a + b = 0 (2)

Subtract (1) from (2):
a = -2
b = 2 - a = 4

Answer: a = - 2 and b = 4

Part 5:
A graph of f(x) with a = -2 and b = 4 is shown below.

Note:
Although f(x) is continuous piecewise, it is not continuous in a mathematical sense.