Answer:
The x-intercept of CD is B(18/5,0). The point C(32,-71) lies on the line CD.
Explanation:
Given information: CD is perpendicular bisector of AB.
The coordinates of point A are (-3, 2) and the coordinates of point B are (7, 6).
Midpoint of AB is C.
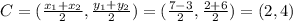
The coordinates of C are (2,4).
The slope of line AB is
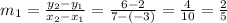
The product of slopes of two perpendicular lines is -1. Since the line CD is perpendicular to AB, therefore the slope of CD is
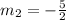
The point slope form of a line is
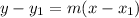
The slope of line CD is
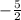 and the line passing through the point (2,4), the equation of line CD is
and the line passing through the point (2,4), the equation of line CD is
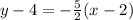
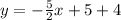
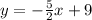 .... (1)
.... (1)
The equation of CD is
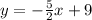 .
.
Put y=0, to find the x-intercept.

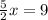

Therefore the x-intercept of CD is B(18/5,0).
Put x=-52 in equation (1).

Put x=-20 in equation (1).
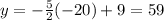
Put x=32 in equation (1).
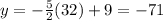
Put x=-54 in equation (1).
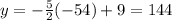
Only point (32,-71) satisfies the equation of CD. Therefore the point C(32,-71) lies on the line CD.