Question

Use the functions a(x)=4x+9 and b(x)=3x-5 to complete the function operations listed below. Part a: find (a+b)(x) show your work. Part b: find (a • b)(x) show your work. Part c: find a[b(x)] show your work.

Answer 1

Parts a and b are straight-forward. You add them in part a: 4x + 9 + 3x - 5 and you get 7x + 4. For part b, you are multiplying them (4x + 9)(3x - 5) by FOILing them:
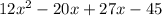
`12 x^(2) -20x+27x-45` which simplifies to
`12 x^(2) +7x-45`
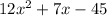
The last one is a composite; you are told to find a of b of x. The way you do that is to take your inside function and put that whole function into the other function every place you see an x, like this:
a(b(x))= 4(3x-5) + 9. Now distribute the 4 into the parenthesis to get 12x - 20 + 9, which simplifies to 12x - 11. And that's it!