2 Answers

Arabia · Answer 1 · 2018-01-11T17:07:23+0000

Answer: The required value of x is 14 and the maesure of angle LMN is 128 degrees.

Step-by-step explanation: As given in the question and shown in the attached figure below, ray MO bisects angle LMN.

Also,

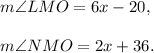
$m\angle LMO=6x-20,\\\\m\angle NMO=2x+36.$

We are to find the value of x and the measure of angle LMN.

Since ray MO bisects angle LMN, so we must have

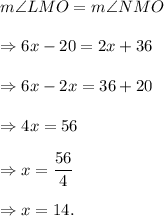
$m\angle LMO=m\angle NMO\\\\\Rightarrow 6x-20=2x+36\\\\\Rightarrow 6x-2x=36+20\\\\\Rightarrow 4x=56\\\\\Rightarrow x=(56)/(4)\\\\\Rightarrow x=14.$

And, we get

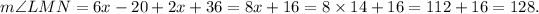
$m\angle LMN=6x-20+2x+36=8x+16=8*14+16=112+16=128.$

Thus, the required value of x is 14 and the maesure of angle LMN is 128 degrees.

Please log in or register to add a comment.