Question

A fair, six-sided die (numbered 1 to 6) is rolled eight times to form an eight-digit number. what is the probability that the resulting number is a multiple of 8? express your answer as a common fraction.

Answer 1

A number is a multiple of 8 if the last 3 digits of it, form a number which is a multiple of 8.

For example: 45288, 16840, 90024 are all multiples of 8, because 288, 840 and 024, the last 2 digits, are multiples of 8.

The total number of 8-digit numbers that we can form using {1,2,3,4,5,6} is
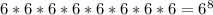
`6*6*6*6*6*6*6*6= 6^(8)`, as we have 6 options for each digit.

The last 3 digits of multiple of 8, formed from the set {1,2,3,4,5,6} can be one of the following:

{112, 136, 144, 152, 216, 224,232, 256, 264
312, 336, 344, 352, 416, 424,432, 456, 464
512, 536, 544, 552, 616, 624,632, 656, 664} ,

which is 27 of them.

For each of these 3 digits fixed in the end, we can form
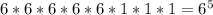
`6*6*6*6*6*1*1*1= 6^(5)` numbers

so in total, there are
`27*6^(5)` numbers divisible by 8, whose digits are numbers in the set {1, 2, 3, 4, 5, 6}.


P(multiple of 8)=n(multiple of 8)/n(numbers that can be formed)=


`(27*6^(5))/(6^(8)) = (27)/(6^(3))= ( (3)/(6) )^(3) =( (1)/(2) )^(3)=0.125`

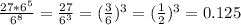
Answer: 0.125