Question

Part A: Solve –mk – 120 > 95 for m. Show your work.

Part B: Solve 2c – 9f = 45 for f. Show your work.

Answer 1

Hello there!

Part A.) Solve -mk - 120 > 95 for m.

First, we need to understand that our primary goal is to isolate m on one side of the inequality.

-mk - 120 > 95
Currently, we have m being multiplied by -k and added to -120.
First, let's cancel out -120 by adding 120 to both sides.
-120 + 120 = 0
95 + 120 = 215

We now have:
-mk > 215
Divide both sides by -k. This is because m is being multiplied by -k. In order to cancel it out, you must perform the opposite order of operations.

-mk / -k = m

Remember, when you divide or multiply a number in an inequality, you must flip the sign to its opposite.

We now are left with:
m
`\leq`
`(215)/(-k)`
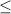
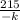This is your solution for part A.

Part B.) Solve 2c - 9f = 45 for f.
Remember that our primary goal is to isolate f on one side of the equation.

2c - 9f = 45
Since -9f is being added to 2c, perform the opposite order or operations on 2c.
+ 2c - 2c = 0

We now have:
-9f = -2c + 45
To solve for f, divide both sides by -9.

f =
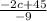
`(-2c + 45)/(-9)` or
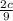
`(2c)/(9)` - 5
This is your solution for part B.)

I hope this helps!

Answer 2

-mk - 120 > 95
-mk > 95 + 120
-mk > 215
m < -215/k
=============
2c - 9f = 45
-9f = -2c + 45
f = 2/9c - 5...or it could be (-2c + 45) / -9