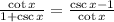Question

Verify the identity. cotangent of x divided by quantity one plus cosecant of x equals quantity cosecant of x minus one divided by cotangent of x

Answer 1

`(\cot x)/(1+\csc x)=(\csc x-1)/(\cot x)`

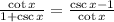
Explanation:

We want to verify the identity:

`(\cot x)/(1+\csc x)=(\csc x-1)/(\cot x)`

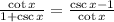
Let us take the LHS and simplify to get the LHS.

Express everything in terms of the cosine and sine function.

`(\cot x)/(1+\csc x)=((\cos x)/(\sin x) )/(1+(1)/(\sin x) )`

Collect LCM

`(\cot x)/(1+\csc x)=((\cos x)/(\sin x) )/((\sin x+1)/(\sin x) )`

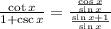
We simplify the RHS to get:

`(\cot x)/(1+\csc x)=(\cos x)/(\sin x+1)`

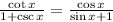
We rationalize to get:

`(\cot x)/(1+\csc x)=(\cos x(\sin x-1))/((\sin x+1)*(\sin x-1))`

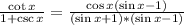
We expand to get:

`(\cot x)/(1+\csc x)=(\cos x(\sin x-1))/(\sin^2 x-1)`

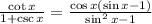
Factor negative one in the denominator:

`(\cot x)/(1+\csc x)=(\cos x(\sin x-1))/(-(1-\sin^2 x))`

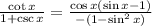
Apply the Pythagoras Property to get:

`(\cot x)/(1+\csc x)=(\cos x(\sin x-1))/(-\cos^2 x)`

Simplify to get:

`(\cot x)/(1+\csc x)=(-(\sin x-1))/(\cos x)`

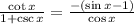
Or

`(\cot x)/(1+\csc x)=(1-\sin x)/(\cos x)`

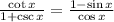
Divide both the numerator and denominator by sin x

`(\cot x)/(1+\csc x)=((1)/(\sin x)-(\sin x)/(\sin x))/((\cos x)/(\sin x))`

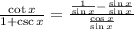
This finally gives:

`(\cot x)/(1+\csc x)=(\csc x-1)/(\cot x)`