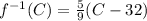Question

The inverse of F(C) = 9 5 C + 32 is

Answer 1

F(C) = 95C + 32...
F(C) is y.
y = 95C + 32
Switch Y & C.
C = 95y + 32
C - 32 = 95y
(C - 32) / 95 = y
In the inverse, y is F-1(C)

F-1(C) = (C - 32) / 95

Answer 2

`f^(-1)(C)=(5)/(9)(C-32)`

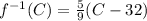
Explanation:

Given : Function
`F(C)=(9)/(5)C+32`

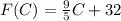
We have to find the inverse of the give function.

Inverse is calculated by putting function f (x) = y ,now taking inverse of f both side , we have,
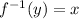`f^(-1)(y)=x` and then finding value of x in terms of x. We obtain inverse of function.

Let
`F(C)=(9)/(5)C+32`

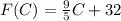
Put F(C) = y ,

then
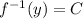`f^(-1)(y)=C` ...........(1)

`y=(9)/(5)C+32`

Subtract 32 both sides, we have,

`y-32=(9)/(5)C`

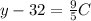
Now multiply both side by
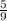`(5)/(9)` , we have,

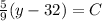`(5)/(9)(y-32)=C` ......(2)

From (1) and (2) , we have,

`f^(-1)(y)=(5)/(9)(y-32)`

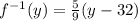
Replace y by C, we have,

`f^(-1)(C)=(5)/(9)(C-32)`