Question

A ship at sea, the Gladstone, spots two other ships, the Norman and the Voyager, and measures the angle between them to be 48°. The distance between the Gladstone and the Norman is 4590 yards. The Norman measures an angle of 55° between the Gladstone and the Voyager. To the nearest yard, what is the distance between the Norman and the Voyager?

Answer 1

use the sine rule:-

x / sin 48 = 4590 / sin (180-48-55)

x / sin 48 = 4590 / sin 103

x = 4590 * sin 48 / sin 103 = 3500.8 yards to nearest tenth

Answer 2

Distance between Voyager and Norman is 3501 yards.

Explanation:

In the figure attached, There are three ships Gladstone, Norman and Voyager based at vertices of a triangle.

Distance between Gladstone and Voyager is 4590 yards, angle between Norman and Voyager is 48° and angle between Gladstone and Voyager is 55°

Since we know m∠N + m∠G + m∠V = 180° [ angles of a triangle ]

So 48 + 55 + m∠V = 180

m∠V = 180 - 103

m∠V = 77°

Now we apply sine rule in the triangle.

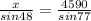
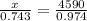
`(x)/(sin48)=(4590)/(sin77)`

`(x)/(0.743)=(4590)/(0.974)`

x =
`(4590*0.745)/(0.974)`

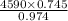
x = 3501.40 ≈ 3501 yards

Therefore, distance between Norman and Voyager is 3501 yards.