Question

The function f(t) = 33 sin (pi over 2t) − 20 models the temperature of a periodic chemical reaction where t represents time in hours. What are the maximum and minimum temperatures of the reaction, and how long does the entire cycle take?

Maximum: 53°; minimum: −13°; period: 4 hours

Maximum: 33°; minimum: 20°; period: pi over 2 hours

Maximum: 13°; minimum: −53°; period: 4 hours

Maximum: 35°; minimum: 35°; period: 8 hours

PLEASE HELP

Answer 1

Maximum is when pi / 2t = 1 so that's 33-20 = 13 degrees
minimum when pi/2t = -1 - that gives -33-20 = -53 degrees

Its C

Answer 2

C. Maximum: 13°; minimum: −53°; period: 4 hours

Explanation:

The function modelling the temperature with respect to time is,

`f(t)=33\sin ((\pi)/(2)t)-20`

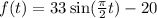
It is required to find the maximum and minimum value of the temperature.

Since, we know,

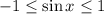`-1\leq \sin x\leq 1` for all values of x.

Then,
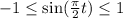`-1\leq \sin ((\pi)/(2)t)\leq 1` for all values of t.

Thus, we get,

Maximum value is obtained when
`\sin ((\pi)/(2)t)=1`

That is,
`\sin ((\pi)/(2)t)=1`,
`f(t)=33-20=13`.

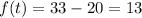So, maximum temperature is 13°

Minimum value is obtained when
`\sin ((\pi)/(2)t)=-1`

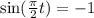
That is,
`\sin ((\pi)/(2)t)=1`,
`f(t)=-33-20=-53`.

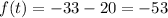So, minimum temperature is -53°

Also, we have,

If the function f(x) has period P, then the function f(bx) will have period
`(P)/(|b|)`.

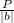Since,
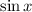`\sin x` has period
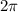`2\pi`, then the given function have period
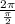`(2\pi )/((\pi)/(2))` = 4.

So, entire cycle takes 4 hours.

Thus, option C is correct.