Question

The sides of a parallelogram are 40 feet and 70 feet long, and the smaller angle has a measure of 36°. find the length of the longer diagonal to the nearest whole number. 44 ft 64 ft 69 ft 105 ft

Answer 1

The answer to this question is:

The sides of a parallelogram are 40 feet and 70 feet long, and the smaller angle has a measure of 36°. find the length of the longer diagonal to the nearest whole number
"105 ft"

Hope this helped, Kernando6867
Your Welcome :)

Answer 2

D. 105 ft.

Explanation:

Please find the attachment.

We have been given that sides of a parallelogram are 40 feet and 70 feet and the smaller angle has a measure of 36 degrees.

Since the measure of all the angles of a parallelogram equals to 360 degrees and opposite angles of parallelogram are equal, so we can find the measure of larger angle of parallelogram as:

`\text{The larger angle of parallelogram}=(360-2* 36)/(2)`

`\text{The larger angle of parallelogram}=(360-72)/(2)`

`\text{The larger angle of parallelogram}=(288)/(2)`

`\text{The larger angle of parallelogram}=144`

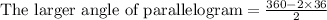
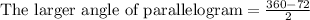
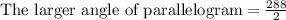
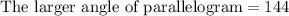
As the larger angle is 144 degrees, so the longer diagonal BD will correspond to 144 degree angle.

Now we will use law of cosines to solve for the length of our longer diagonal (BD) as.

`c^2=a^2+b^2-2*a*b*cos(C)`

Upon substituting our given values in above formula we will get,

`(BD)^2=70^2+40^2-2*70*40*cos(144)`

`(BD)^2=4900+1600-5600*(-0.809016994375)`

`(BD)^2=6500+4530.4951685`

`(BD)^2=11030.4951685`

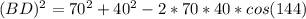
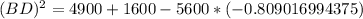
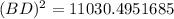
Let us take square root of both sides of our equation.

`BD=√(11030.4951685)`

`BD=105.0261\approx 105`

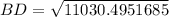
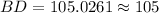
Therefore, the longer diagonal is 105 ft and option D is the correct choice.