Question

Diberikan bilangan asli 3,5,8,12,17,23,30,38,47..... rancang suatu formula untuk mencari suku ke 400 dan lanjutkan dgn induksi matematika

Answer 1

google translate - indonesian:

"Given the original numbers design a formula to find the 400th term and continue (prove) with mathematical induction"

Let
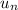
`u_n` represent the n'th term of the sequence, that is


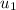
`u_1` is the first term,
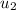
`u_2` the second term and so on...

notice that :


`u_1=3`


`u_2=3+2`


`u_3=3+2+3`


`u_4=3+(2+3+4)`


`u_5=3+(2+3+4+5)`

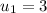
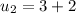
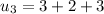
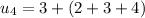
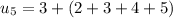
so clearly


`u_n=3+(2+3+4+5...+n)=2+(1+2+3+...+n)`

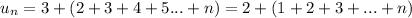
Recall the famous Gauss formula for addition of the first consecutive n natural numbers: 1+2+3+...(n-1)+n=n(n+1)/2

then, the formula for u_n is:


`u_n=2+(1+2+3+...+n)=2+ (n(n+1))/(2)`

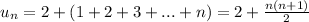
for example, the 5th term is :


`u_5=2+ (5(5+1))/(2)=2+15=17`


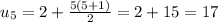
Proof by induction.

step 1

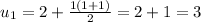
`u_1=2+ (1(1+1))/(2)=2+1=3`, true

step2

assume true for n=k, that is assume
`u_k=2+ (k(k+1))/(2)`

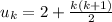
step 3

verify for n=k+1, that is verify that
`u_k_+_1=2+ ((k+1)(k+2))/(2)`.



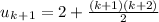
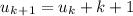
`u_k_+_1=u_k+k+1}` because each nth term of the sequence is clearly its previous term +n

for example the fourth term 12, is the third term +4.

the fifth term, 17, is the fourth term 12 + 5 and so on...

also, by our assumption
`u_k=2+ (k(k+1))/(2)`

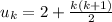
so:


`u_k_+_1=u_k+k+1=2+ (k(1+1))/(2)+k+1=2+(k(1+1))/(2)+ (2(k+1))/(2)`
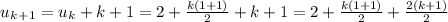
factorizing k+1


`=2+ ((k+1)((k+2))/(2)`

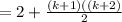
which is what we needed to show.


Answer:
`u_n=2+ (n(n+1))/(2)`