Question

Let v1=(3,5) and v2=(-4,7) Compute the unit vectors in the direction of |v1| and |v2|?

Answer 1

By definition, the unit vector of v = (a,b) is

`\hat{v} = \frac{\vec{v}}`

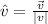
Therefore,
The unit vector of v₁ = (3,5) in the direction of |v₁| s
(3,5)/√[3² + 5²]
= (3,5)/√34

The unit vector of v₂ in the direction of |v₂| is
(-4,7)/√[(-4)² + 7²]
= (-4,7)/√65

Answer:
The unit vector of v₁ in the direction of |v₁} is
`( (3)/(√(34)) , (5)/(√(34)) )`
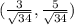
The unit vector of v₂ in the directin of |v₂| is

`( (-4)/(√(65)) , (7)/(√(65)) )`