Question

A blimp is 1100 meters high in the air and measures the angles of depression to two stadiums to the west of the blimp. If those measurements are 75.2° and 17.9°, how far apart are the two stadiums?

Answer 1

Answer: 3115.03301179982 meters

This value is approximate

-----------------------------------------------
-----------------------------------------------

Refer to the image attachment

Segments
AB = 1100 meters = height of blimp
DE = x meters = distance between stadiums
AD = y meters
AE = AD+DE = y+x

Angles
Angle ADB = angle CBD = 75.2 degrees
Angle CBE = angle BEA = 17.9 degrees

Focus on triangle ADB
tan(angle) = opposite/adjacent
tan(D) = AB/AD
tan(75.2) = 1100/y
y*tan(75.2) = 1100
y = 1100/tan(75.2)
y = 290.632536450073

Focus on triangle AEB
tan(angle) = opposite/adjacent
tan(E) = AB/AE
tan(E) = 1100/(y+x)
tan(17.9) = 1100/(290.632536450073+x)
0.32299119934583 = 1100/(290.632536450073+x)
0.32299119934583(290.632536450073+x) = 1100
93.8717515169298+0.32299119934583x = 1100
0.32299119934583x = 1100-93.8717515169298
0.32299119934583x = 1006.12824848308
x = 1006.12824848308/0.32299119934583
x = 3115.03301179982

This answer is approximate

Answer 2

3315.03 meters.

Explanation:

We have been given a blimp is 1100 meters high in the air and measures the angles of depression to two stadiums to the west of the blimp. We are asked to find the distance between both stadiums.

First of all, we will find the distance between 1st stadium and base of blimp. We can see that stadium and blimp forms a right triangle with respect to ground, where m is adjacent side and 1100 meters is opposite side for 75.2 degrees angle. So we can set an equation as:

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(75.2^(\circ))=(1100)/(m)`

`m=\frac{1100}{\text{tan}(75.2^(\circ))}`

`m=(1100)/(3.784848088366)`

`m=290.632536`

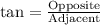
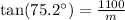
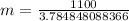
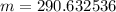
Similarly, we will find value of x as:

`\text{tan}(17.9^(\circ))=(1100)/(m+x)`

`\text{tan}(17.9^(\circ))=(1100)/(290.632536+x)`

`290.632536+x=\frac{1100}{\text{tan}(17.9^(\circ))}`

`290.632536+x=(1100)/(0.322991199346)`

`290.632536+x=3405.6655482`

`290.632536-290.632536+x=3405.6655482-290.632536`

`x=3115.033`

`x\approx 3115.03`

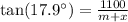
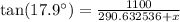
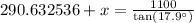
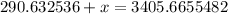
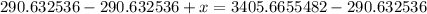
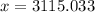
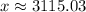
Therefore, the two stadiums are approximately 3115.03 meters apart.