Step-by-step explanation:
The given data is as follows.
n = 0.020 moles, P = 1.5 atm
T = 290 K, molar mass of nitrogen = 14.0 g/mol
R = 8.314 J/mol, d = ?
It is known that the relation between density, pressure, and temperature is as follows.
P =
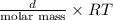
Putting the given values into the above relation and calculate the density as follows.
P =
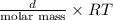
1.5 atm =
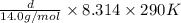
d =
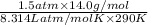
=
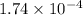 g
g
Thus, we can conclude that density of the given gas is
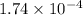 g.
g.