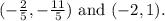To solve the given system of equations we will use the substitution method.
Subtracting 2x from the first equation we get:
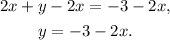
Substituting the above equation in the second one we get:

Simplifying the above equation we get:
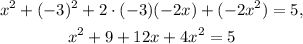
Adding like terms we get:
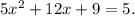
Subtracting 5 from the above equation we get:
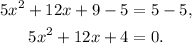
Now, notice that:
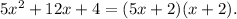
Therefore:
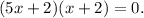
Now, we know that:
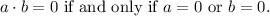
Therefore:
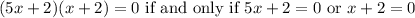
Then:
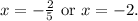
Finally, substituting the above result in y=-3-2x we get:
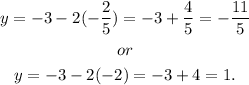
Therefore, the solutions of the given system of equations are:
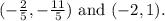
Answer: