Question

O is the center of the circle. Assume that lines that appear to be tangent are tangent. What is the value of x?

Answer 1

hello :
29° +90°+X° = 180°
x° = 180°-90°-29°
x° = 61°...(first answer)

Answer 2

(A)
`x=61^(\circ)`

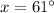
Explanation:

Given: O is the center of the circle and ∠OPQ=29°.

To find: The value of x.

Solution:

We know that A tangent to a circle forms a right angle with the circle's radius, at the point of contact of the tangent, therefore ∠OQP=90°.

Now, using the angle sum property in ΔOPQ, we ahve

`{\angle}OPQ+{\angle}PQO+{\angle}QOP=180^(\circ)`

Substituting the given values, we get

⇒
`29^(\circ)+90^(\circ)+x=180^(\circ)`

⇒
`119^(\circ)+x=180^(\circ)`

⇒
`x=61^(\circ)`

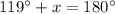
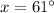
Hence, the value of x is 61 degrees.

Thus, option A is correct.