Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar. One of the x-intercepts of the parabola represented by the equation y = 3x2 + 6x − 10 is approximately (1.08, 0). The other x-intercept of the parabola is approximately . (Round your answer to the nearest hundredth.) NextReset

Answer 1

Explanation:

The equation is given as:

`y=3x^2+6x-10`

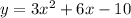
has 2 x-intercepts which can be found out by putting y=0 or by just solving the given equation.

But it is given that one of the x-intercept is 1.08.

For the above given equation
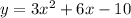`y=3x^2+6x-10`, sum of the roots is:

`(-b)/(a)=(-6)/(3)=-2`.

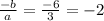Let the other x-intercept be p, then

`p+1.08=-2`

⇒
`p=-2+1.08`

⇒
`p=-3.08`

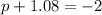
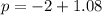
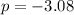
therefore, the another x intercept is (-3.08,0).

Answer 2

3x^2 + 6x - 10 = 0
3(x^2 + 2x) - 10 = 0
3[ (x + 1)^2 - 1 ] - 10 = 0
3(x+1)^2 - 13 = 0

so the vertex is at (-1,-13)
the roots will be same distance from x = -1
that is a distance 1.08 --1 = 2.08

so other root is approximately -1 -2.08 = -3.08

the other intercept is at (-3.08,0)