Prove {0,2,0,2,0,2,...} does not converge

Question

asked Apr 19, 2018 177k views

1 Answer

Dupree · Answer 1 · 2018-04-26T02:41:21+0000

Recall that a sequence
x_n

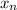
is convergent if and only if
x_n

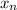
is also a Cauchy sequence, which means to say that for any
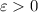
$\varepsilon>0$ , we can find a sufficiently large

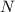
for which

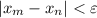
$|x_m-x_n|<\varepsilon$

whenever both

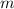
and

exceed

.

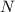
But this never happens if we choose
m=n+1

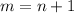
and
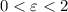
$0<\varepsilon<2$ ; under these conditions, we have

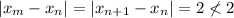
$|x_m-x_n|=|x_(n+1)-x_n|=2\\ot<2$

Therefore
x_n

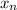
is not a Cauchy sequence and hence does not converge.