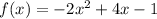
To find a maximum or minimum, we have to derivate our function and set it equal to 0
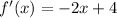
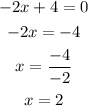
Now that we have the point at x, we plug it into the initial function f(x) to find the point at y
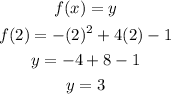
Now we know that our maximum or minimun point is (2,3)
To know if it is a maximum or a minimum we must perform the second derivative. Remember that if the sign of the second derivative is negative, our point is a maximum and if it is positive, our point is a minimum.
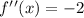
Now we know that our point is a maximum since its second derivative was negative. This can be seen in the graph, where our function belongs to a parabola that opens downwards
For the domain and range we have:
• The ,domain, of the function that is equivalent to all the values that x can take are, all the real ones
,
• The ,range, of the function that is equivalent to all the values it can take on and is defined from its maximum point to negative infinity, that is ,[3,-∞)