Question

If x>2, then x^2-x-6/x^2-4=

Answer 1

consider the expression
`(x^(2) -x-6)/( x^(2) -4)`

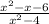
To factorize the expression in the denominator we use difference of squares:
`x^(2) -4=x^(2) - 2^(2) =(x-2)(x+2)`

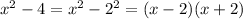
To factorize
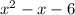
`x^(2) -x-6` we use the following method:


`x^(2) -x-6=(x-a)(x-b)`

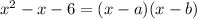
where a, b are 2 numbers such that a+b= -1, the coefficient of x,

and a*b= -6, the constant.

such 2 numbers can be easily checked to be -3 and 2

(-3*2=6, -3+2=-1)

So
`x^(2) -x-6=(x-a)(x-b)=(x+3)(x-2)`


`(x^(2) -x-6)/( x^(2) -4)= ((x+3)(x-2))/((x-2)(x+2))= (x+3)/(x+2)`



`(x+3)/(x+2)= (x+2+1)/(x+2)= (x+2)/(x+2)+ (1)/(x+2)=1+ (1)/(x+2)`

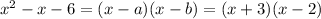
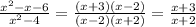
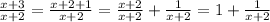
for x>2


`(1)/(x+2)\ \textless \ (1)/(2+2)= (1)/(4)`

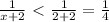
thus

for x>2,


`1+ (1)/(x+2)\ \textless \ 1+ (1)/(4)= (5)/(4)`


Answer:

for x>2


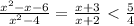
`(x^(2) -x-6)/( x^(2) -4) = (x+3)/(x+2) \ \textless \ (5)/(4)`, (but the expression is never 0)