Question

Write the sum using summation notation, assuming the suggested pattern continues.

2 - 12 + 72 - 432 + ...

Answer 1

`\displaystyle \sum_(k=1)^(n)2(-6)^(k-1)`

Explanation:

we have to write the sum using summation notation of the following series:

2-12+72-432+...

which could also be written as:

2+(-12)+72+(-432)+...

We observe that first term=2

second term=2×-6

Third term=2×-6×-6

Fourth term=2×-6×-6×-6

nth term=
`2* (-6)^(n-1)`

Hence, the series sum=
`\displaystyle \sum_(k=1)^(n)2(-6)^(k-1)`

Answer 2

Answer:
`\displaystyle \sum_(k=1)^(n)2(-6)^(k-1)`

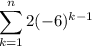
The first term is a = 2. The common ratio is r = -6. You start off with 2 and multiply each term by -6 to get the next term.

eg: 2*(-6) = -12 ---> -12*(-6) = 72 etc etc

If you want the series summation to go on forever, then replace the 'n' up top with the infinity symbol
`\infty`

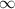
Note: Because |r| < 1 is not true (r < 1 in this case), this means that the series diverges.