Question

Find the coordinates of point S that lies along the directed line segment from R(-14, -1) to T(4, -13) and partitions the segment in the ratio of 1:5.

Answer 1

Answer: The required co-ordinates of the point S are (-11, -6).

Step-by-step explanation: We are given to find the co-ordinates of the point S that lies along the directed line segment from R(-14, -1) to T(4, -13) and partitions the segment in the ratio of 1:5.

We know that

the co-ordinates of a point that divides the line segment joining the points (a, b) and (c, d) in the ratio m : n is given by

`\left((mc+na)/(m+n),(md+nb)/(m+n)\right).`

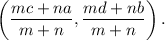
According to the given information, we have

(a, b) = (-14, -1), (c, d) = (4, -13) and m : n = 1 : 5.

Therefore, the co-ordinates of the point S are given by

`\left((1*4+5*(-14))/(1+5),\frac{1*(-13)+5*(-1)}{}\right)\\\\\\=\left((4-70)/(6),(-13-5)/(6)\right)\\\\\\=\left((-66)/(6),(-18)/(6)\right)\\\\=(-11,-3)`

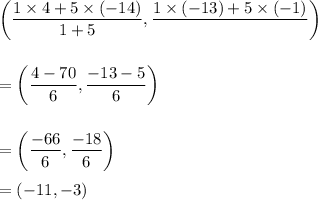
Thus, the required co-ordinates of the point S are (-11, -6).

Answer 2

check the picture below.

I'd like to point out, is 1:5 from R to T, since that matters, that way we know the ratio from RS is the 1 and the ratio ST is the 5.


`\bf \left. \qquad \right.\textit{internal division of a line segment} \\\\\\ R(-14,-1)\qquad T(4,-13)\qquad \qquad 1:5 \\\\\\ \cfrac{RS}{ST} = \cfrac{1}{5}\implies \cfrac{R}{T} = \cfrac{1}{5}\implies 5R=1T \implies 5(-14,-1)=1(4,-13)\\\\ -------------------------------\\\\`


`\bf { S=\left(\cfrac{\textit{sum of`