Question

Solve for x under the assumption that x>0

X-7/x <-6

Answer 1

Good evening:


Assuming (x - 7)/x < -6

We need x ≠ 0.

Adding 6 to both sides:


`\mathsf{(x-7)/(x)+6\ \textless \ -6+6}\\ \\ \mathsf{(x-7)/(x)+6\ \textless \ 0}`

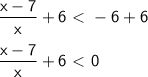
We put the expression in the same denominator:


`\mathsf{(x-7)/(x)+(6x)/(x) \ \textless \ 0}\\ \\ \\ \mathsf{(x + 6x-7)/(x)\ \textless \ 0}\\ \\ \\ \mathsf{(7x - 7)/(x) \ \textless \ 0}\\ \\ \\ \mathsf{7\cdot(x - 1)/(x) \ \textless \ 0} \ \ \ \ \ \ \mathsf{(/ 7)}\\ \\ \\ \mathsf{(x-1)/(x) \ \textless \ 0}`

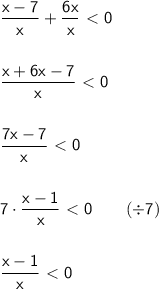
Now we need to study the signal of the numerator and denominator:


x - 1 = 0
x = 1 → When N = 0, x = 1.

x - 1 > 0 → x > 1
x - 1 < 0 → x < 1

x = 0 → D = 0 when x = 0
x > 0 → D > 0 when x > 0
x < 0 → D < 0 when x < 0

Now we build a table with the numerator and denominator signals:

N: - - - - - - - - - - - - - - -- - 1 + + + + + +
D: - - - - - - - - 0 + + + + + + + + + + + +

N/D + + + + + 0 - - - - - - - - 1 + + + + + +

Therefore, we have that (x - 1) / x < 0 when 0 < x < 1



`\texttt{Solution: \ x}\in\mathbb{R}\mathtt{: x}\in\texttt{(0,1)}`