Question

A soccer ball is kicked toward the goal. The height of the ball is modeled by the function h(t) = -16t^2 + 48t where t equals the time in seconds and h(t) represents the height of the ball at time t seconds. What is the axis of symmetry, and what does it represent?

Answer 1

Good evening.

The simetry axis can be found with the vertex in x formula:


`\mathsf{x_V = -(b)/(2a)}`


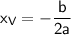
Whe take from the function:

a = -16
b = 48

So:


`\mathsf{t_v = -(48)/(2\cdot (-16))}\\ \\ \mathsf{t_v = (-48)/(-32)}\\ \\ \\ \boxed{\mathsf{t_v = (3)/(2)}}`


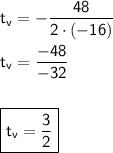
We can conclude that the axis of simetry is the line with the equation:

t = 3/2

It represents that if we take two points at the same x-distance to this line, they will have the same image(value in h).


For example:

t' = 3/2 + 1/2 = 4/2 = 2
t'' = 3/2 - 1/2 = 2/2 = 1

We calculate h(t):


`\mathsf{h(x') = -16.{1}^2+48.1}\\ \\ \mathsf{h(x') = -16 + 48 = 32}\\ \\ \\ \mathsf{h(x'') = -16.2^2 + 48.2}\\ \\ \mathsf{h(x'')=-64 + 96=32}`

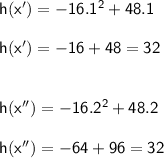
Where we can se the same h-value.


Doubts? Please, comment :)