Answer: The correct answer is

Explanation:
A Quadratic equation is defined as the equation in which the highest power of the variable is 2. The general form of this equation represents:

where,

From the given options:
1.
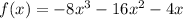 : Here, the highest power of the variable is 3. Therefore, it is not a quadratic equation.
: Here, the highest power of the variable is 3. Therefore, it is not a quadratic equation.
2.
 : Here, the highest power of the variable is 2. Therefore, it is a quadratic equation.
: Here, the highest power of the variable is 2. Therefore, it is a quadratic equation.
3.
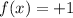 : Here, the highest power of the variable is 0. Therefore, it is not a quadratic equation.
: Here, the highest power of the variable is 0. Therefore, it is not a quadratic equation.
4.
 : Here, the highest power of the variable is 1. Therefore, it is not a quadratic equation.
: Here, the highest power of the variable is 1. Therefore, it is not a quadratic equation.
Hence, the correct answer is
