Question

Hugh akston took out a 30 year mortgage with an ear of​ 5.9%. if hugh borrowed​ $300,000 to buy his​ home, then his monthly payment will be closest​ to:

Answer 1

The formula of the present value of an annuity ordinary is
Pv=pmt [(1-(1+r/k)^(-kn))÷(r/k)]
Pv present value 300000
PMT monthly payment?
R interest rate 0.059
K compounded monthly 12 because the payments are monthly
N time 30 years
Solve the formula for PMT
PMT=pv÷ [(1-(1+r/k)^(-kn))÷(r/k)]
PMT=300,000÷((1−(1+0.059÷12)^(
−12×30))÷(0.059÷12))
=1,779.41

Answer 2

Monthly payment = $1,779.41

Step-by-step explanation:

A mortgage is a a form of loan that is secured on a specified property that the debtor with predetermined periodic payments over a fixed period of time.

Here is the formula for calculating Hugh's monthly repayment

`\\P[(r(1+r)^n)/(((1+r)^n)-1))]`

Explanation of the terms below

• P = Loan amount.

• M = Monthly mortgage payment.

• r = Interest rate. Which has to be recalculated to monthly. Therefore monthly rate[5.9% expresssed in percentage] =
  `(0.059)/(12)` = 0.004917
• n = number of payments. This is the loan term. Therefore our N = 30 years by 12 months = 360.

Fitting into the formular:

`\\300000 * (0.004917(1+0.004917)^'360')/((1+0.004917)^'360')-1`

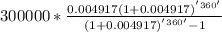
Which is = $1779.41 monthly