consider the function

the x-intercepts of the graph of f, are the zeros of f, that is the solutions of f(x)=0.
so we solve
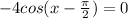

at this point we ask ourselves, keeping the unit circle in mind, "cosine of what is 0?"
In the unit circle, from 0 to 2π radians,
cos 90° = cos (π/2) rad = 0
and
cos 270° = cos (3π/2) rad = 0
this means that
i)


and
ii)

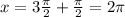
ii) also, check that
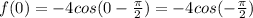
is also 0, because cos (-pi/2)= cos (-90°)=cos 270°=0
Answer:
x=0, x=π, and x=2π