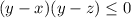Answer: choice D)
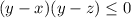
=====================================================
Step-by-step explanation:
Unfortunately, we don't have enough info to determine what x,y, and z are.
However, we do know that x < y < z is the case. Though to be more technical, x = y or y = z could be possible, but for now we'll ignore these cases.
So we'll focus on x < y < z.
This is true because 25% of the values are below x and 50% of the values are below y. So naturally x is smaller than y. Also, 75% of the values are smaller than z, so z is the largest of the three values.
Since x < y, this makes 0 < y-x when you subtract x from both sides. This is the same as saying y-x > 0. So y-x is positive.
On the other hand, because y < z, this leads to y-z < 0. So y-z is negative.
We have
- y-x is some positive value
- y-z is some negative value
therefore, (y-x)(y-z) = (positive)*(negative) = negative
Overall,
(y-x)(y-z) < 0
So far, we can see that we have strict inequality. However, it is possible to have x = y or y = z be possible. Consider a set like {5,5,5,7,9}. You should find that Q1 = 5 and Q2 = median = 5 also. This example is one of infinitely many where x = y. Due to something like this, we must update (y-x)(y-z) < 0 into