Question

Determine the value of a so that the line whose equation is ax+y-4=0 is perpendicular to the line containing the points (2,-5) and (-3,2)

Answer 1

First, write the equation of the line containing the points (2,-5) and (-3,2).

We can use 2 point form, or point-slope form.

Let's use point-slope form.

the slope m is
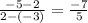`(-5-2)/(2-(-3))= (-7)/(5)`, then use any of the points to write the equation. (ex, pick (2, -5))

y-(-5)=(-7/5)(x-2)

y+5=(-7/5)x+14/5

y= (-7/5)x+14/5 - 5 =(-7/5)x+14/5 - 25/5 =(-7/5)x-11/5


Thus, the lines are

i) y=-ax+4 and ii) y=(-7/5)x-11/5

the slopes are the coefficients of x: -a and (-7/5),

the product of the slopes of 2 perpendicular lines is -1,

so

(-a)(-7/5)=-1

7/5a=-1

a=-1/(7/5)=-5/7


Answer: -5/7