Question

A regular pentagonal prism has a height of 14 in. and a base edge length of 10 in. Identify its lateral area and surface area.

Can anyone help me solve this?

Answer 1

L = 700 in2 ; S = 1044.1 in2

Explanation:

Lucky guess :)

Answer 2

The lateral faces of the prism are 5 rectangles with dimensions 10 by 14.

So the lateral area = 5 * 10 * 14 = 700 (in squared)


Consider one of the bases of the prism.

As shown in the figure, the pentagon is made up of 5 isosceles triangles.

The vertex of each of these 5 triangles is 360°/5=72°.

Draw the altitude, which forms 2 right triangles with angle measures 36°-54°-90°.

Let he hypotenuse be s and the altitude be h in, as shown in the figure.

x*cos54°=5

x=5/(cos54°)=5/(0.588)=8.5

then,

h=x*sin54°=8.5*(0.8)=6.8 (in)

Thus, the area of one of the 5 congruent isosceles triangles is


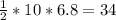
`(1)/(2)*10*6.8= 34` (in squared)

The area of the pentagonal base is 34*5 = 170 (in squared)


Thus the surface area = lateral area + 2 base area
= 700+2*170 = 700+340 = 1040 (in squared)


Answer:

lateral area: 700 in squared

surface area: 1040 in squared