Answer: The average rate of change of f(t) from t = 2 to t = 6 is 1.5 thousand owners per year.
Explanation:
Given: The function below shows the number of car owners f(t), in thousands, in a city in different years t:
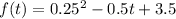
Now,
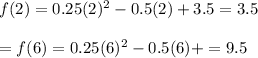
Now, the average rate of change of f(t) from t = 2 to t = 6 is given by :-

Hence, the average rate of change of f(t) from t = 2 to t = 6 is 1.5 thousand owners per year.