Answer:
Option B
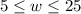
Explanation:
Let
L------> the long of the cardboard piece
W-----> the width of the cardboard piece
The area of cardboard piece is equal to

In this problem we have

so
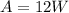
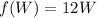 ------> equation A
------> equation A
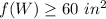 ------> inequality B
------> inequality B
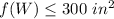 ------> inequality C
------> inequality C
Substitute equation A in the inequality B

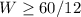

Substitute equation A in the inequality C
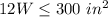
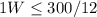
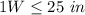
The domain for the function f(W) is equal to the interval------>
![[5,25]](https://img.qammunity.org/2018/formulas/mathematics/middle-school/zbl0gb2lcixzcz13ix9hj6yyam7vgo8p5t.png)