Question

Advanced Functions: estimate the slope of the tangent to the graph of the function y= 2x^3 + x^2 + 23 at X= 2How do I estimate the slope of a tangent?

Answer 1

The slope of the tangent to the graph of a function at x=x₀ can be estimated by finding the slope of a line that passes through two points near to x₀.

For instance, evaluate the function f at x₀+h and x₀. The slope will be given by:

`m=(f(x_0+h)-f(x_0))/((x_0+h)-(x_0))=(f(x_0+h)-f(x_0))/(h)`

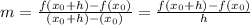
For small values of h, this slope will approach the slope of the tangent line.

For the given function:

`f(x)=2x^3+x^2+23`

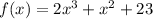
Use x₀=2 and h=0.01. Then, we must evaluate f at x=2.01 and at x=2:

`\begin{gathered} f(2)=2(2)^3+(2)^2+23=43 \\ f(2.01)=2(2.01)^3+(2.01)^2+23=43.281302 \end{gathered}`

Then, the slope of the tangent line is approximately:

`m\approx(f(2.01)-f(2))/(0.01)=(43.281302-43)/(0.1)=28.1302`

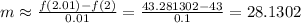
We can get better approximations by choosing smaller values for h. For instance, if h=0.001, we would get:

`m\approx(f(2.001)-f(2))/(0.001)=(43.028013-43)/(0.001)=28.013\ldots`

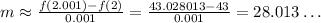
Therefore, the slope of the line tangent to the graph of y=2x³+x²+23 is approximately 28.