Question

Find all values of $x$ such that $6= \dfrac{35}{x} -\dfrac{49}{x^2}$. If you find more than one value, then list your solutions in increasing order, separated by commas.

Answer 1

x=7/3 and x=7/2

if you want the step-by-step then you just try to isolate x and it is pretty self-explanatory from there on. Hope this helped!

:P

Answer 2

`x=(7)/(3) , (7)/(2)`

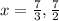
Explanation:

`6= (35)/(x) - (49)/(x^2)`

Now we need to solve for x

To get 'x' alone we make the denominators same

LCD = x^2

WE multiply the whole equation by x^2

`6x^2 = 35x - 49`

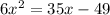
Now we the equation =0, move all the terms to left hand side

`6x^2-35x + 49=0`

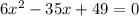
Now we apply quadratic formula to solve for x

a= 6, b= -35 , c= 49

`x= (-b+-√(b^2-4ac))/(2a)`

`x= (-(-35)+-√((-35)^2-4(6)(49)))/(2*6)`

`x= (35+-√(49))/(12)`

`x= (35+-7)/(12)`

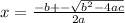
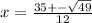
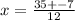
Now frame two equations , one with + and another with -

`x= (35+7)/(12)`
`x= (35-7)/(12)`

`x= (42)/(12)`
`x= (28)/(12)`

`x= (7)/(2)`
`x= (7)/(3)`

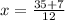
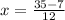
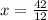
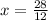
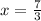
So value of x= {7/3, 7/2}