1.
Given any 2 points P(a, b) and Q(c, d), the midpoint
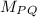
of PQ is given by
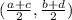
.
2.
Let the x coordinates of the vertices of P_1 be :
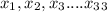
the x coordinates of P_2 be :
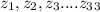
and the x coordinates of P_3 be:

3.
we are given that
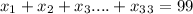
and we want to find the value of
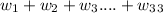
.
4.
According to the midpoint formula:
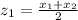
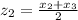
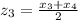
.
.
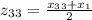
and
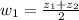
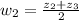
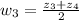
.
.
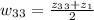
5.
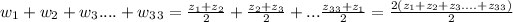
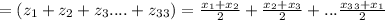
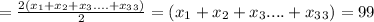
Answer: 99