Question

Three cube-shaped boxes are stacked one above the other. The volumes of two of the boxes are 1,331 cubic meters each, and the volume of the third box is 729 cubic meters. What is the height of the stacked boxes in meters?

Answer 1

Answer: The height of the stacked boxes is 31 meters.

Explanation:

Since, the Volume of a cube = (side)³

The volume of first box = 1331 cubic meters,

⇒ (side)³ = 1331

⇒

Similarly, the side of second box = 11 meters ( Because, both boxes have the same volume )

Now, the volume of third box = 729 cubic meters

⇒ ⇒ (side)³ = 729

⇒

Thus, the height of the stacked boxes = Side of first box + side of second box + side of third box

= 11 + 11 + 9

= 31 meters.

Answer 2

The volume of a box with dimensions x by x by x is
`x^(3)`.

So if we are given the volume V of a cube-shaped box, the side length of thit is
`\sqrt[3]{V}`.

So we calculate the cubic roots of the volumes we have, and we add their heights.

To calculate the cubic root of 729, we can factorize it, and group the perfect cubes together, as follows:


`(729)/(3)= (600)/(3) + (120)/(3) + (9)/(3)=200+40+3=243`


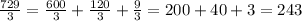
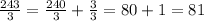
`(243)/(3)= (240)/(3)+ (3)/(3)=80+1=81`, which we recognize as
`3^(4)`

so
`729=3*3* 3^(4)= 3^(6)= ( 3^(2) )^(3)= 9^(3)`

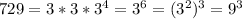
similarly 1,331 can be found to be
`11^(3)`.

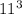
Thus we have 2 boxes with side length equal to 11 m and one with side length equal to 9 m.


Answer: h= 11+11+9 = 31 (meters)