Question

Choose the linear inequality that describes the graph. The gray area represents the shaded region

Answer 1

(1,0)(0,-2)
slope = (-2 - 0) / (0 - 1) = -2/-1 = 2

y int (where the line crosses the y axis) = (0,-2)

equation is : y = 2x - 2.....line is solid, so there is an equal sign in the problem....shading is above the line, so it is greater then

ur inequality is : y > = 2x - 2

Answer 2

The required inequality that shown in the given graph is
`y\geq 2x-2`.

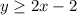Explanation:

Consider the provided graph.

The y-intercept of the line is, (0,-2)

The x-intercept of the line is, (1,0)

To find the equation of line use the formula:

`(y-y_1)=(y_2-y_1)/(x_2-x_1)(x-x_1)`

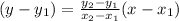
Substitute
`(x_1,y_1)=(0,-2)\text{and}(x_2,y_2)=(1,0)`

`y-(-2)=(0-(-2))/(1-0)(x-0)`

`y+2=((2))/(1)(x)`

`y+2=2x`

`y=2x-2`

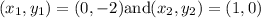
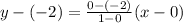
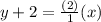
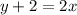
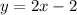
Therefore the equation of line is
`y=2x-2`.

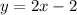The graph is solid line and shaded region is above the line. So, use the inequality sign "≥".

Thus, the required inequality that shown in the given graph is
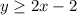`y\geq 2x-2`.