Question

Find the area of a regular hexagon with apothem 2√3 mm. Round to the nearest whole number.

Answer 1

Join the center of the hexagon with the 2 base angles.

An equilateral triangle, with side length x, is formed.

(remark: a regular hexagon is made up of 6 equilateral triangles with equal length)

The height
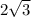
`2 √(3)` forms 2 congruent right triangles with :

hypotenuse= x, side_1=x/2, and side_2=
`2 √(3)`.

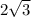
From the pythagorean theorem we have:


`x^(2) = ( (x)/(2) )^(2)+(2 √(3))^(2)`


`x^(2) = ( x^(2) )/(4) +12`


`(3)/(4) x^(2) =12`


`x^(2) = (12*4)/(3)=4*4`

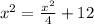
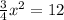
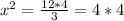
thus, x=4.

The area of the triangle is 1/2 * 4 *
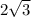
`2 √(3)`=6.93 (mm squared)

The area of the hexagon is 6* the area of the triangle = 42 (mm squared)


Answer: a. 42 (mm squared)