Question

What is the factorization of the polynomial graphed below? Assume it has no constant factor.

A. (x+5)(x+5)
B. (x-5)(x-5)
C. x-5
D. x+5

Answer 1

Remember that the solutions, or zeroes, or roots of a function are the points where the function outputs zero. In other words, if
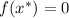`f(x^*) = 0`, then
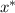`x^*` is a solution/zero/root of
`f(x)`. If this is the case, then the function can be factored as the multiplication of parenthesis like
`(x-x^*)`.

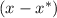As a graphical consequences, the zeroes of a function correspond to the points
`x = x^*,\ y = 0`, and all points like
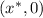`(x^*,0)` are on the x-axis.

So, the graph of a function touches the x axis at
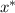`x^*` if and only if
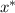`x^*` is a solution for the function.

Now, your graph represents a parabola. A parabola can either have:

- No solutions, meaning that it never touches the x axis

- Two coincident solutions, meaning that it touches the x axis "twice", in the same point

- Two different solutions, meaning that it crosses the x axis in two different points.

You parabola has two coincident solutions, because it only touches the x axis twice at
`x = 5`.

This means that
`x = 5` is twice a solution of the parabola, and as such, it implies the factorization
`(x-5)(x-5) = (x-5)^2`