Question

Find the polynomial f(x) that has the roots of -2, 5 of multiplicity 2. Explain how you would verify the zeros of f(x).

Answer 1

If -2 is a root of f, then (x-(-2))=(x+2) is a factor of f

similarly, if 5 is a root of f, then (x-5) is a factor of f(x).

These roots have multiplicity 2 means that there are 2 of each,

so f(x) is written as (x+2)(x+2)(x-5)(x-5)


`f(x)= (x+2)^(2) (x-5)^(2)`

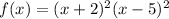
[the most general form is f(x)= c*(x+2)^{2} (x-5)^{2}*P(x), where c is a constant and P(x) another polynomial]

To show that -2 and 5 are zeros of f, we must prove that f(-2)=0 and f(5)=0,

Using the function we wrote:


`f(-2)= (-2+2)^(2) (-2-5)^(2)=0* (-7)^(2)=0`

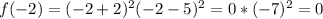
similarly:


`f(5)= (5+2)^(2) (5-5)^(2)=0`