Question

Sketch a 30-60-90 triangle. If the longest side of a similar triangle one foot, then how many inches is the shortest side?

Answer 1

Given that the angles of the triangle are 30, 60, and 90.

Using the sine law

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

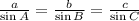
Substitute A=30, B=60, and C=90, we get

`(a)/(\sin 30^o)=(b)/(\sin 60^o)=(c)/(\sin 90^o)`
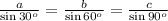
`\text{Substitute }\sin 30^o=(1)/(2),\sin 60^o=\frac{\sqrt[]{3}}{2},\text{ and }\sin 90^o=1,\text{ we get}`

`(a)/((1)/(2))=\frac{b}{\frac{\sqrt[]{3}}{2}}=(c)/(1)`

`2a=\frac{2b}{\sqrt[]{3}}=c`

We know that the longest side should be the opposite side of the big angle (90).

Let c be the longest side of the given triangle.

Substitute c=1, we get

`2a=\frac{2b}{\sqrt[]{3}}=1`
`2a=1\text{ and }\frac{2b}{\sqrt[]{3}}=1`

`a=(1)/(2)\text{ and }b=\frac{\sqrt[]{3}}{2}`
`a=0.5\text{ and b=}0.866`

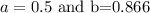
The smallest side is 0.5 feet

Conver the feet into inches.

`1\text{ foo}t\text{ =12 inches }`

Dividing both sides by 2, we get

`(1)/(2)\text{ foo}t\text{ =}(12)/(2)\text{ inches }`

`0.5\text{foo}t\text{ =}6\text{ inches }`

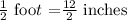
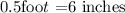
Hence the smallest side is 6 inches.