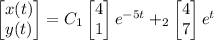I assume the coefficient on

in the second equation is
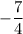
. The coefficient matrix
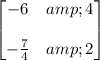
has eigenvalues given by
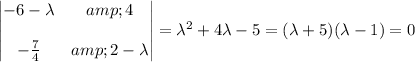
The eigenvalues are thus

and
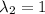
.
For the eigenvalue
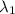
, the corresponding eigenvector
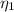
satisfies
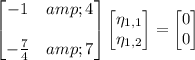
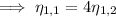
so that we can choose

.
For
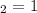
, we have
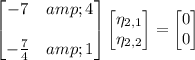

and we can choose
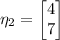
for the corresponding eigenvector.
Then the general solution to the ODE system is given by